ICLR 2025 | Air-DualODE: 知识数据双驱动的开放系统空气质量预测

本文介绍华东师范大学决策智能实验室被ICLR2025录用的知识数据双驱动的最新工作，该工作与香港科技大学（广州）、华为诺亚方舟实验室研究团队合作完成。

作者： 田锦东，梁宇轩，徐榕荟，陈鹏，郭晨娟，周傲英，潘璐珈，饶仲文，杨彬

关键词： 时空序列预测，知识数据双驱动，开放空气系统

论文链接： https://openreview.net/pdf?id=kOJf7Dklyv

代码链接： https://github.com/decisionintelligence/Air-DualODE

摘要：空气污染严重威胁着人类健康和生态系统，因此迫切需要有效的空气质量预测来指导公共政策。传统方法通常分为基于物理的模型和基于数据驱动的模型。基于物理的模型通常面临高计算成本和封闭系统假设的限制，而数据驱动的模型可能忽略已知的物理动力学，使得时空相关性的建模变得困难。尽管一些物理引导的方法尝试结合两类模型的优势，但往往存在显式物理方程与隐式学习表示之间的不匹配问题。为了解决这些挑战，我们提出Air-DualODE，一种新颖的物理引导方法，它利用了双分支的神经微分方程（Neural ODE）进行空气质量预测。分支一采用开放空气系统的物理方程，捕捉时空依赖关系以学习物理动态系统；分支二则采用纯数据驱动的方式，补充物理分支中未能涉及的依赖关系。最后，这两个分支的深度表征在时间上进行对齐并融合，以提高预测精度。实验结果表明，Air-DualODE在不同空间尺度的污染物浓度预测中达到了SOTA，为解决实际空气质量预测问题提供了一种有前景的解决方案。

动机

空气污染对人类健康和生态环境构成了严重威胁，精准的空气质量预测对于公共政策制定至关重要。现有的空气质量预测方法主要分为基于物理模型的方法和数据驱动的方法。然而，这两类方法各自存在明显的局限性。

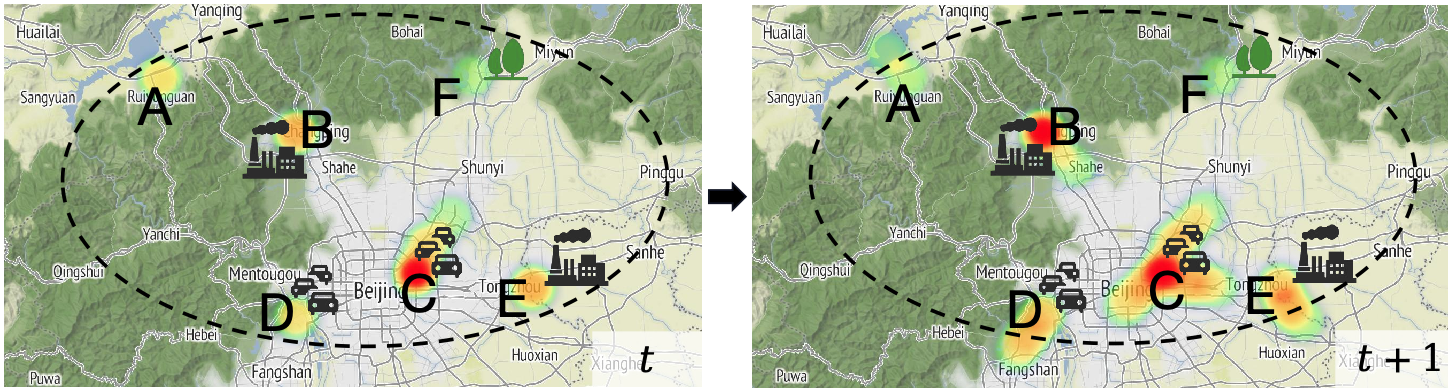
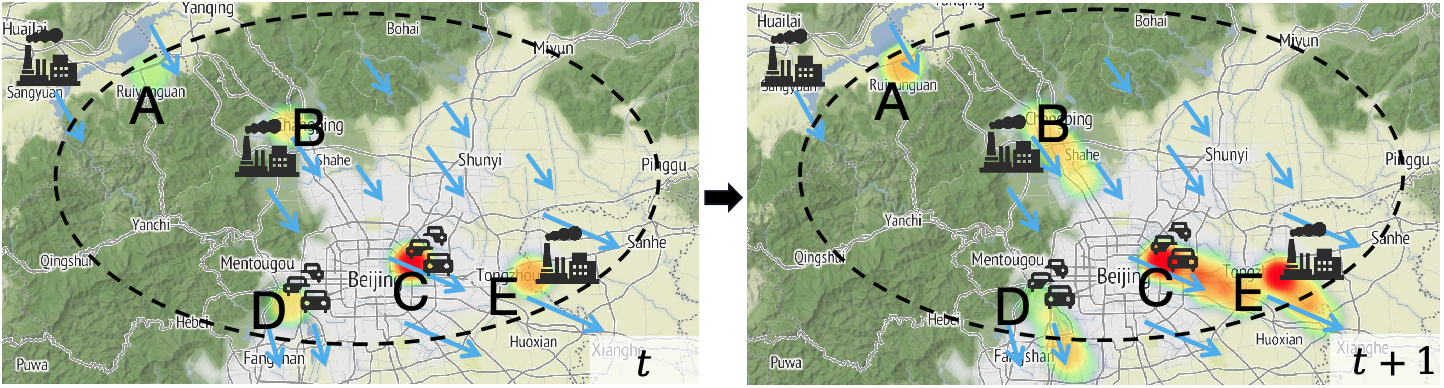
基于物理模型的方法：依赖常微分方程（ODEs）或偏微分方程（PDEs）来模拟污染物的扩散和输运过程。这些方法虽然具备较强的理论解释能力，但在大规模计算时往往面临高昂的计算成本。此外，传统物理模型通常假设空气污染是封闭系统，即污染物总量随时间保持不变，而这与真实世界的空气流动情况不符（如图1所示）。
数据驱动的方法：通过深度学习模型从历史数据中挖掘污染物浓度的时空依赖关系。这类方法能够很好地发现数据之间的关系，但由于其缺乏物理约束导致模型捕捉到不完整甚至错误的时空依赖深度表征。

a.污染物随着浓度扩散传播

b.污染物随着风场对流传播

图1：站点污染物浓度随时间变化的热力图。

挑战

因此，很有必要提出一种知识数据双驱动的深度学习模型，结合物理模型和纯数据驱动模型的优势。但目前开发这种模型还面临着两个重大挑战：

物理方程在开放空气系统中的不现实假设：现有的空气质量预测通常采用连续性方程（Continuity Equation）模拟污染物传播，但该方程基于封闭系统假设，即污染物总量随时间保持不变。尽管这一假设在交通流建模、流行病传播等领域有效，但在空气质量预测中并不适用。在真实世界中，污染物传播是一个复杂的开放系统，污染物能够随风飘入/飘出研究区域（如图1中的A、D、E）。此外，污染物也会因为工业排放、交通污染而产生（图1中的B、C、D、E）；还会因为森林和湖泊作用而消散（图1.a中的A、F）。正是由于开放空气系统的复杂性，导致封闭系统假设的传统物理方程在开放系统中的适用性受到严重限制，甚至会引入错误的归纳偏置（Inductive Bias），影响模型的预测精度。
显式物理方程与隐式深度学习表征的不匹配：物理方程提供了一种可解释的建模方式，能够精确描述污染物浓度的变化，并确保每个变量都有清晰的物理含义。然而，深度学习方法采用隐式表征来学习污染物的时空依赖关系，这些表征由物理变量的非线性变换得到，难以直接映射到现实的物理量。因此，如何在数据驱动模型中合理地引入物理知识，同时避免两者的不匹配，是知识数据双驱动模型面临的核心挑战。

方法概述

为了将扩散-对流方程（污染物传播方程，通过连续性方程导出）融入神经网络，并确保正确的时序时空依赖性。我们提出了Air-DualODE，一种全新的知识数据双驱动模型，该模型为包括物理方程和数据驱动的双分支动态系统。

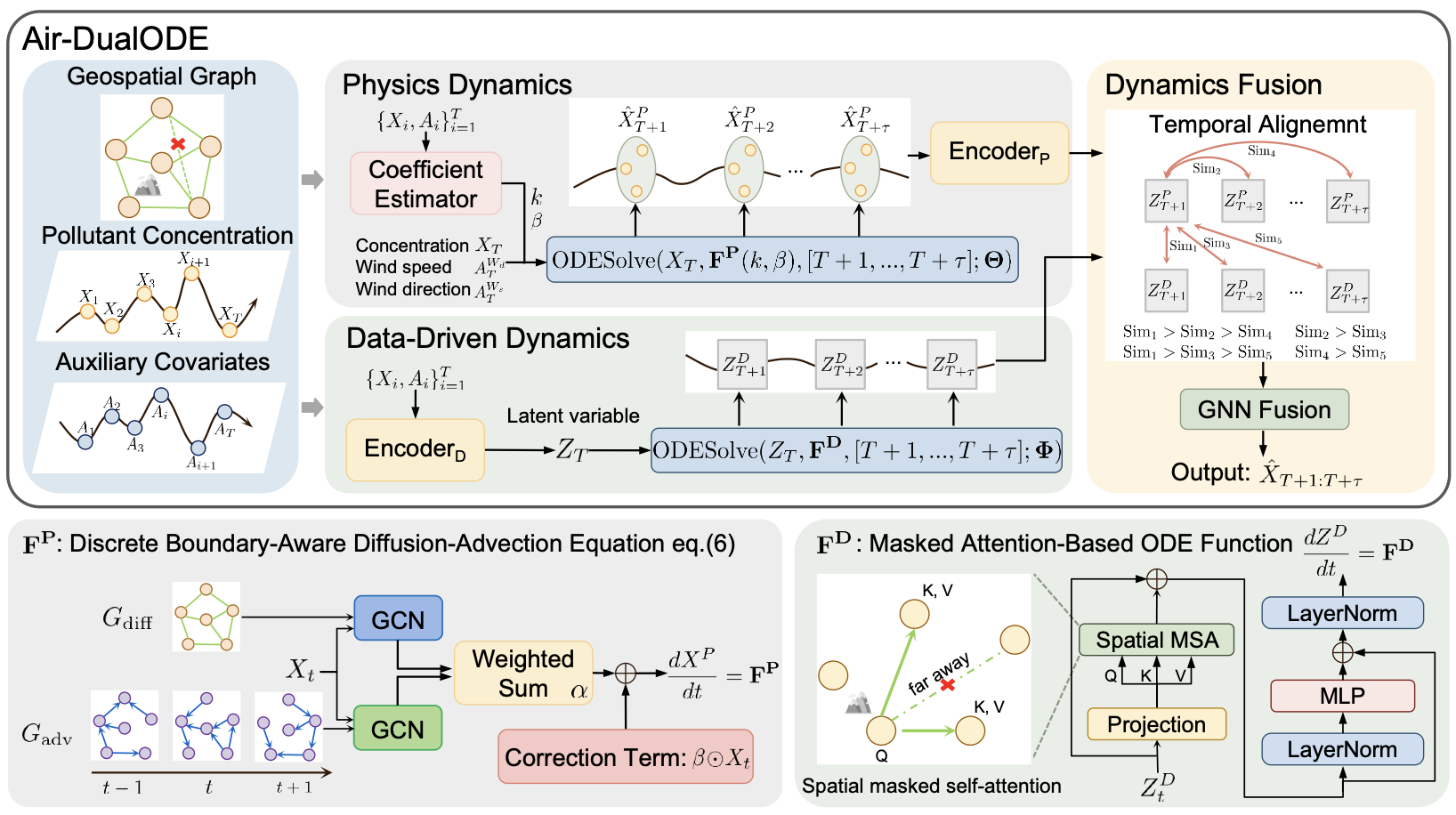
图2：Air-DualODE架构图，由物理动态系统，数据驱动动态系统和动态系统表征融合，三个部分组成。

物理动态系统：为了保持与神经网络隐式表征的一致性，物理分支直接求解物理方程，获取具有物理意义的时序关联。具体而言，它求解基于开放空气系统的空间离散化常微分方程，即 $\mathbf{F^P}$ ，用于生成未来 $\tau$ 步的物理模拟结果 $\hat{X}^P_{T+1:T+\tau}$ 。然后，这些结果被映射到隐空间，得到 $Z^P_{T+1:T+\tau}$ 。

数据驱动动态系统：尽管物理分支捕捉了符合现实污染物变化的时空依赖，但它并没有考虑未被方程建模的时空关联，比如：温度和湿度对污染物传播的影响，以及时序特征模式之间的联系。为了解决这个问题，数据驱动分支通过带有空间掩码注意力机制的神经微分方程实现，即 $\mathbf{F^D}$ 。这个分支捕获了潜在空间中的未知动态系统，并生成潜在的动态表示 $Z^D_{T+1:T+\tau}$ 。

动态系统表征融合：尽管 $Z^P_{T+1:T+\tau}$ 和 $Z^D_{T+1:T+\tau}$ 都在隐空间并拥有相同的时间跨度，但它们尚未对齐。为了解决这个问题，衰减时序对比学习模块通过衰减的权重在时间上对齐它们，从而实现有效融合。然后，图神经网络在变量维度融合这两种动态系统表征，融合后的结果被解码生成最终预测结果 $\hat{X}_{T+1:T+\tau}$ 。

物理分支

扩散-对流方程（Diffusion-Advection Equation）通过连续性方程导出，描述了污染物分别因为污染物浓度扩散和风场对流产生的自然传播现象。
$\frac{\partial X}{\partial t} = k \cdot \nabla^2 X - \vec{\nabla} \cdot (X \cdot \vec{v}).$
其中， $X$ 是污染物浓度； $k$ 是扩散系数； $\vec{v}$ 是风场； $\nabla^2$ 是拉普拉斯算子， $\vec{\nabla}$ 为散度算子。
离散化扩散-对流方程（Discrete Diffusion-Advection Equation，DAE）为扩散-对流方程在封闭系统中的离散化形式。通过空间离散化（Method of Lines），可以将上述偏微分方程离散化为站点粒度的常微分方程，如下式所示：
$\frac{d X}{d t}=-k \cdot L_{\mathrm{diff}} X+L_{\mathrm{adv}} X.$
其中， $L_{\text{diff}}$ 和 $L_{\text{adv}}$ 分别为扩散和对流的离散化拉普拉斯算子；前者为静态图，而后者为根据风场变化的动态图。根据封闭系统假设，可以得出结论：
$\sum_{i=1}^N \frac{d X_i}{d t} = 0,$
$N$ 为站点个数。这表明污染物的总量是恒定不变的，但这显然与现实情况不符。
边界感知的离散化扩散-对流方程（Boundary-Aware Diffusion-Advection Equation，BA-DAE）移除了封闭系统假设，考虑了开放系统中污染物的产生与消散，如下式所示：
$\mathbf{F^P}(X_t; \mathbf{\Theta}) = \frac{dX}{dt} = \boldsymbol{\alpha} \odot (-k \cdot L_{\text{diff}} X) + (1 - \boldsymbol{\alpha}) \odot (L_{\text{adv}} X) + \boldsymbol{\beta} \odot X.$
其中， $\boldsymbol{\alpha}$ 为线性层估计得到的权重，用以表示扩散和对流对污染物传播的影响程度； $\boldsymbol{\beta} \odot X$ 为针对开放系统设计的修正项。

通过使用ODE求解器求解BA-DAE，可获得未来时刻的污染物浓度，并通过时间编码器将其映射到隐空间，以进行动态系统表征融合，如图 2中的物理分支所示。

\hat{X}^P_{T+1:T+\tau} = \text{ODESolve}(X_T, \mathbf{F^P}, [T+1, ..., T+\tau]; \mathbf{\Theta}), \\ Z^P_{T+1:T+\tau} = \text{Encoder}_\text{P} (\hat{X}^P_{T+1:T+\tau}).

需要注意的是， $Z^P_{T+1:T+\tau}$ 编码了物理方程所描述的污染物传播时空依赖，数据驱动模型并不能保证完全捕捉。因此弥补了数据驱动方法的缺陷并在一定程度上增强了模型的可解释性。

数据驱动分支

该分支主要用于建模BA-DAE以外的动态系统，以捕捉无法仅通过物理方程描述的污染物传播。例如，BA-DAE可能难以精准建模历史数据中的时空依赖关系，而数据驱动分支能够从历史数据中学习这些潜在的动态特性；类似湿度对污染物传播等复杂关系，也可以通过该分支进行有效建模。模型设计采用隐空间神经微分方程进行动态建模，以 $(X, A)_{1:T}$ （历史污染物浓度和辅助变量，如气象数据）作为输入。通过 $\text{Encoder}_\text{D}$ 将输入映射到隐变量 $Z^D_T$ 作为初始状态并进行求解：

Z^D_T = \text{Encoder}_\text{D}(X_{1:T}, A_{1:T}), \\ Z^D_{T+1:T+\tau} = \text{ODESolve}(Z^D_T, \mathbf{F^D}, [T+1, ..., T+\tau]; \mathbf{\Phi}).

此外，由于站点之间污染物传播并非任意，本文还在 $\mathbf{F^D}$ 中加入了空间掩码注意力机制，使用地理邻接矩阵 $G$ 作为掩码，确保没有直接联系的站点不会相互影响。

动态系统表征融合

衰减时序对比学习模块通过定义软权重，对齐 $Z^P$ 和 $Z^D$ ，从而解决两者在隐空间不匹配不一致问题，并使得融合更加有效。

先定义衰减时序权重：

w(t, s) = \left\{\begin{matrix} 2 \cdot \sigma(-\lambda_1 \cdot |t - s|) & \text{if } \ |t - s| < \tau \\ 2 \cdot \sigma(-\lambda_2 \cdot |t - s \bmod \tau|) & \text{if } \ |t - s| > \tau. \end{matrix}\right.

再定义衰减时序对比学习损失：

p(t, t')=\frac{\exp \{ \text{Sim}(\mathcal{\bar{Z}}_{t}, \mathcal{\bar{Z}}_{t'} ) \} } { \sum_{i=1, i \neq t'}^{2 \tau} \exp \{ \text{Sim}(\mathcal{\bar{Z}}_t, \mathcal{\bar{Z}}_i) \} }.

\ell(t)=-\log p(t, t+\tau) - \sum_{j=1, j \neq\{t, t+\tau\}}^{2 \tau} w(t, j) \cdot \log p(t, j).

最后，该模块的损失函数如下：

\mathcal{L}_{\text{tcl}}=\frac{1}{2\tau} \sum_{t=1}^{2\tau} \ell(t).

图神经网络融合基于空间关系图 $G$ ，将对齐后的两类表征进行融合，最终总损失函数如下所示：

\mathcal{L} = \frac{1}{\tau} \sum_{t=T+1}^{T+\tau} \| X_t - \hat{X}_t \| + \gamma \mathcal{L}_{\text{tcl}}.

实验结果

整体性能

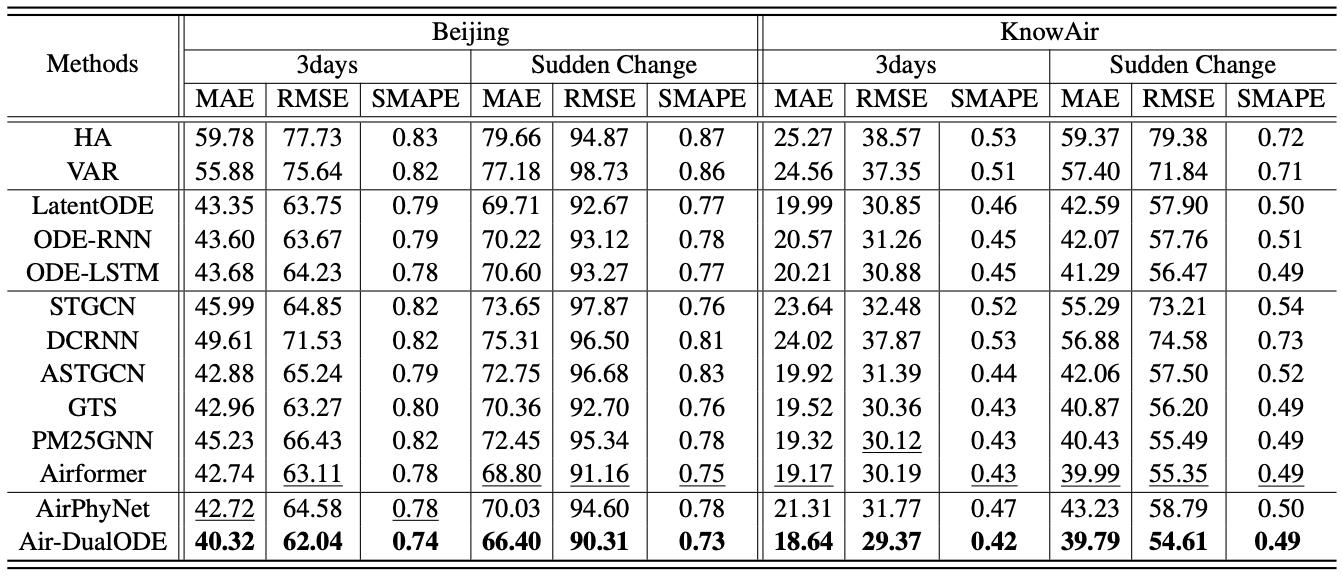
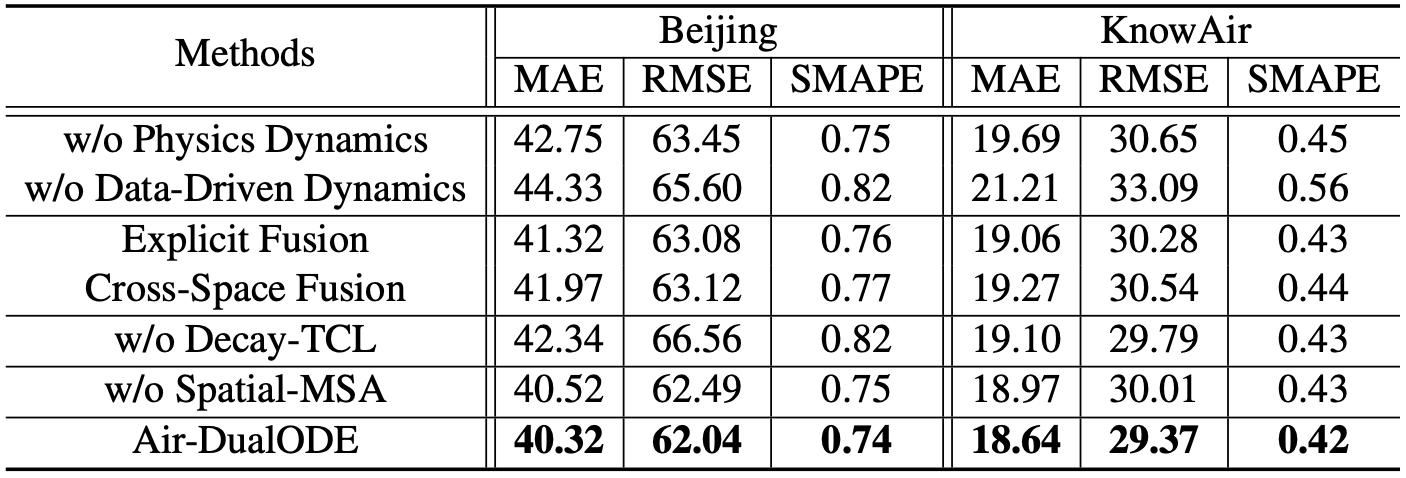
如表1所示，Air-DualODE在Beijing（城市级别）和KnowAir（全国级别）两个不同粒度的数据集上的三天预测结果和突变预测结果都超过了现有模型。这表明模型将物理分支和数据驱动分支结合后能够捕捉复杂的时空依赖关系。

表1：在两个数据集上整体预测结果对比。粗体为最好结果，下划线为次好结果。

消融实验

不仅如此，本文还进行了详尽的消融实验以证明Air-DualODE各个模块的有效性。

双分支动态系统：如表二所示，双分支相辅相成，不能缺失任意一方。
隐空间融合：如表二所示，物理驱动与数据驱动的融合需要在同一空间，隐空间融合效果好于显空间融合。
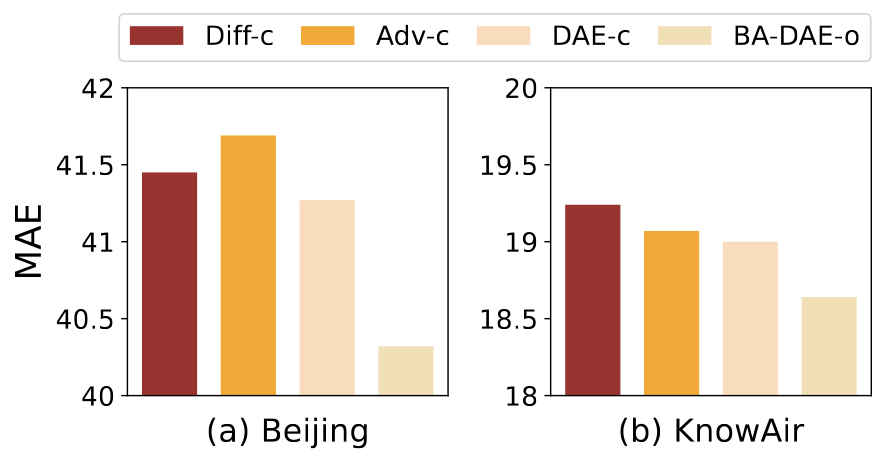
物理知识：如图三所示，在物理分支上使用不同的物理知识会得到不一样的效果，这体现了物理知识正确性非常重要。
空间掩码注意力机制：如表二所示，远距离的站点表征并不会提供有用的信息。
衰减时序对比学习：如表二所示，表明两类表征在融合前需要在隐空间对齐。

表2：消融实验结果。

图3：物理分支使用不同的物理知识所带来的效果

总结

本文设计了Air-DualODE用于城市级和国家级的空气质量预测，这是首个针对开放空气系统的双动力学模型。模型采用双动力学方法，使用Neural ODEs分别建模物理（已知）和数据驱动（未知）的动力学，并在隐空间中对齐并融合这两种动力学，从而有效地将物理知识与数据驱动方法结合起来。与以往的物理引导方法相比，Air-DualODE能够适用于城市级和国家级数据集进行空气质量预测。未来，我们计划进一步探索物理引导的DualODE架构，并将其扩展到更一般的时空预测任务。

欢迎大家关注华东师范大学数据科学与工程学院决策智能实验室

官网：decisionintelligence.github.io

知乎：DI DaSE ECNU

公众号：DI DaSE ECNU